Table of Contents
- Author(s) of this documentation:
- David Coeurjolly
Introduction
This documentation page is dedicated to distance and metric computations in DGtal. As discussed in nD Volumetric Analysis using Separable Processes, distance functions play an important role in volumetric analysis of shapes (distance transformation, Voronoi maps, medial axis,...). We formalize here the concepts related to such function. First of all, let us start with main definitions:
- Definition:
- \((E, F, d)\) is a metric space if \(d\) is a map from \(E\) to a subgroup \(F\) of \(\mathbb{R}\) such that \(\forall a,b,c\in E\),
- (non-negative) \( d(a,b)\geq 0\)
- (identity of indiscernibles) \( d(a,b)= 0 \Leftrightarrow a=b\)
- (symmetry) \(d(a,b)=d(b,a)\)
- (triangular inequality) \(d(a,c) \leq d(a,b) + d(b,c)\)
When performing some geometry processing, one may consider additional requirements on the metric and thus norms:
- Definition:
- Given a vector space EV, a norm is a map \(g\) from \(EV\) to a subgroup \(F\) of \(\mathbb{R}\) such that \(\forall \vec{x},\vec{y}\in EV\),
- (non-negative) \( g(\vec{x})\geq 0\)
- (identity of indiscernibles) \( g(\vec{x})= 0 \Leftrightarrow \vec{x}=\vec{0}\)
- (triangular inequality) \(g(\vec{x}+\vec{y}) \leq g(\vec{x}) + g(\vec{y})\)
(homogeneity) \( \forall \lambda\in\mathbb{R}, \quad g(\lambda\cdot\vec{x}) = |\lambda|\cdot g(\vec{x})\)
\(d(a,b):= g(b-a)\) is the metric induced by the norm \(g\).
In the following, we restrict our attention to metric spaces even if some of them are induced by norms.
Main concepts
In DGtal, the concept of CMetricSpace is associated with metric space definition. A first refinement of this concept is the concept of CDigitalMetricSpace whose models implement distance functions on integer numbers (i.e. \((\mathbb{Z}^n, \mathbb{Z}, d)\)). For example,
- LpMetric are models of CMetricSpace on \((\mathbb{R}^n, \mathbb{R}, d)\) spaces (i.e. all computations are performed on C++ "double").
- \( l_p\) metrics (ExactPredicateLpSeparableMetric or InexactPredicateLpSeparableMetric) are models of CMetricSpace on \((\mathbb{Z}^n, \mathbb{Z}, d)\) for \(p>1\) with specific separability methods.
- Chamfer norms with axis symmetric unit ball (see experimental::ChamferNorm2D in dimension 2).
- DigitalMetricAdapter which adapts any metric (model of CMetricSpace) to digital space using the ceil function. This induces a digital metric (ceil function preserves the triangular inequality).
For instance, CMetricSpace requires to have a binary operator to compute the distance between any two points of the digital space. Furthermore, it requires to have a method he closest(origin,p,q) which returns the closest point from p and q to the origin. Such closest method can be easily implemented from the binary distance operator. However, for some metric, more efficient implementation can be obtained to answer to closest() requests.
- Note
- Models of CMetricSpace concept also implements a rawDistance(x,y) method. This method returns a value of type RawValue which may be considered as an exact representation of the distance between x and y. For example, if we consider a \( l_p\) metric, the distance between x and y can be represented as sum of power p terms (the distance without the order p square root). Hence, if RawValue is an exact type (e.g. model of CInteger with enough capacity to represent power p integers), rawDistance method can be used to perform exact metric comparison. To sum up for any instance metric of the class ExactLpSeparableMetric for instance:
- metric(x,y) returns the distance as double, i.e. \(\left ( \sum_{i=1}^n |x_i-y_i |^p \right )^{\frac{1}{p}}\)
- metric.rawDistance(x,y) returns the power p of the distance as an integer DGtal::int64_t (default type), i.e. \( \sum_{i=1}^n |x_i-y_i |^p\)
Similarly to metric models, Power Metrics are important for reverse distance reconstruction and medial axis extraction. For \( l_2\) metric, the power distance between a point \( x\) and a ball \((y,r)\) with centger \(y\) and radius \(r\), is defined by
\[ pow(x,y) = \| x - y\|_2^2 - r \]
Power values may be negative but the geometry of the distance (convex unit balls,...) are relevant in volumetric analysis.
SeparableMetric Concept
We perform volumetric analysis using separable approaches (see nD Volumetric Analysis using Separable Processes), additional properties are required for the model of metrics (see [71], [52], [33]).
Such properties are related to a monotonicity property of the metric. In dimension 2, consider two points \( p(x,y)\), \(q(x',y')\) with \(x<x'\). Let \(r( x'',0)\) be a point on the x-axis such that \(d(p,r) = d(q,r)\) and \( s(u,0)\) be another point on the x-axis. A metric \( d\) is monotonic if
\[ u < x'' \implies d(p,s) \leq d(q,s) \]
and
\[ u > x'' \implies d(p,s) \geq d(q,s) \]
As discussed in [52], any metric induced by a norm with axis symmetric unit ball is monotonic. Hence, all \(l_p\) are monotonic, as well as most path based norms (chamfer norms, neighborhood sequence norms,...). Such properties are implemented in the concept of CSeparableMetric. Similarly, CPowerSeparableMetric can be defined as a refinement of CPowerMetric with monotonicity property of the power metric.
The separable metric concept is a refinement of the CMetricSpace (resp. CPowerMetric) concept in which we require models to implement a method hiddenBy(u,v,w,startingPoint,endPoint,dim): given three digital points u, v, w and an isothetic segment defined by the pair [startingPoint, endPoint] along the dimension dim, such method returns true if Voronoi cells of u and w hide the Voronoi cell if v on the segment. Such predicate can be illustrated as follows:
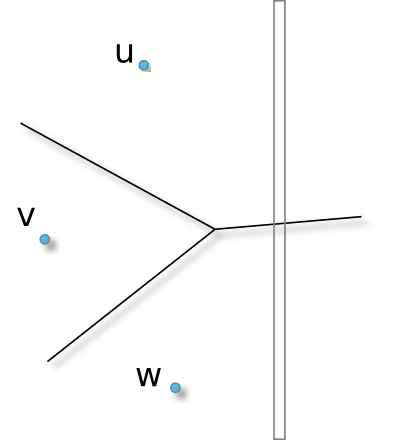
This predicate (with the closest() one as discussed above) is crucial for separable VoronoiMap/DistanceTransformation algorithms. The next section discusses about complexity of such volumetric algorithm with respect to computation costs of the two predicates.
CPowerSeparableMetric concepts is a similar refinement of the CPowerMetric concept. Indeed, CPowerSeparableMetric models must implement an hiddenByPower(u, wu,v,wv,w,ww,startingPoint,endPoint,dim) on triplet of weighted points {(u,wu),(v,wv),(w,ww)}.
The class SeparableMetricAdapter adapts any model of CMetricSpace which is monotonic to a model of CSeparableMetric. Please refer to the following table for computational costs.
Main models and Computational Costs for Volumetric Analysis
Main models of CSeparableMetric and CPowerSeparableMetric are:
- ExactPredicateLpSeparableMetric: main class for \( l_p\) metrics (with exact predicates)
- InexactPredicateLpSeparableMetric: main class for \( l_p\) metrics (with approximated predicates)
- SeparableMetricAdapter: adapts any model of CMetricSpace (with
- monotonicity property) to CSeparableMetric
- ExactPredicateLpPowerSeparableMetric: main class for power \( l_p\) functions (with exact predicates).
- experimental::ChamferNorm2D: proof-of-concept of separable volumetric computation from path based norms.
As discussed in nD Volumetric Analysis using Separable Processes, both VoronoiMap and PowerMap (and their associated subclasses) are parametrized by a generic separable metric (model of CSeparableMetric or CPowerSeparableMetric). If \( C \) corresponds to the cost of the closest() or closestPower() methods for the given metric, and \( H \) the cost of the hiddenBy() or hiddenByWeigthed() in dimension \( n \), the computational costs of the separable metrics can be summarized as follows (for a domain of size \( N^n \)):
| Models of CSeparableMetric/CPowerSeparableMetric | C | H | Note |
|---|---|---|---|
| \( O(\log(p)) \) | \( O(\log(p)\cdot\log(N)) \) | Exact computations | |
| ExactPredicateLpSeparableMetric specialized for p=2 | \( O(n) \) | \( O(n) \) | Exact computations |
| ExactPredicateLpSeparableMetric specialized for p=1 | \( O(n) \) | \( O(n \cdot \log(N)) \) | Exact computations (H could be implemented in \( O(n) \)) |
| InexactPredicateLpSeparableMetric with p at construction | \( O(n) \) | \( O(n \cdot \log(N)) \) | Inexact computations since std::pow on double is used (supposed to be \( O(1) \)) |
| \( O(n\cdot \log(p)) \) | \( O(n\cdot \log(p) \cdot \log(N)) \) | Exact computations | |
| ExactPredicateLpPowerSeparableMetric specialized for p=2 | \( O(n) \) | \( O(n) \) | Exact computations |
| SeparableMetricAdapter of a metric aMetric | \( O(m) \) | \( O(m \cdot \log(N)) \) | relies on aMetric(p,q) computations in \( O(m) \) (the metric must satisfy some constraints, see [33]) |
| experimental::ChamferNorm2D | \( O(\log(p)) \) | \( O(\log^2(N)) \) | [33] |
Following this table, VoronoiMap and DistanceTransformation have the following computational cost:
\[ O(n\cdot N^n\cdot (C+H)) \]
The same complexity holds for PowerMap and ReverseDistanceTransformation for \( l_p\) metrics.
For example, for the \( l_2 \) metric, all algorithms are in \( O(n^2N^n)\).