Table of Contents
- Author(s) of this documentation:
- Tristan Roussillon
In this example, we show how to test a length estimator of the contour of a generated shape, which is digitized at different resolutions.
Please have a look to shapeGridCurveEstimator.cpp to get the complete source code of this tutorial.
Implicit Gauss digitization of a Euclidean shape
Let us assume that a flower-like shape has been instanciated.
We now implicitely consider its digitization according to the Gauss scheme (set of digital points lying inside the shape).
- Note
- Similarly to the previous tutorial (Tutorial "Image -> Region -> Grid curve -> Length estimation"), the explicit construction of the digital set is not necessary.
Since the shape knows its bounding domain, it is enough to have a predicate that indicates, for each point of the domain, whether it belongs to the digital set or not. This is a useful feature when we want to digitize a shape at a high resolution. - The grid step h is given in the init method of the GaussDigitizer. The smaller the grid step, the higher the resolution is.
Tracking, grid curve, range
The extraction of the contour is performed in a cellular space (with 0-, 1-, and 2-cells), given an adjacency (0-, 1-, 2-adjacency). See Cellular grid space and topology, unoriented and oriented cells, incidence for the basic concepts of cellular topology.
Since there is only one connected digital set, a fast method is used to find a first boundary element (i.e. a 1-cell between a 2-cell inside the shape and a 2-cell outside the shape). Instead of scanning the whole domain, points are randomly tested, until one point inside the shape and one point outside the shape are found. A dichotomic process is then used to retrieve the boundary element that is lying between these two points.
- Note
- A DGtal::InputException is raised if the method fails to find two different points.
From one boundary 1-cell, the contour is then implicitely tracked as follows:
The GridCurve object is merely built from the retrieved contour:
Here is a picture of the contour:

Length estimation
The DSS approach chosen below for the length estimation requires a points range:
Similarly to the previous tutorial (Tutorial "Image -> Region -> Grid curve -> Length estimation"), we initialize the DSS length estimator from the points range and get the estimated length.
Note that there is a specific length estimator, which is called true length estimator, because it returns the true length (or a very close value to the true length). The only difference between the true estimator and the other ones is that the true estimator knows the shape and its parameters.
Thanks to the true estimator, it is very easy to compare the accuracy of the estimators against a ground truth. In our example, we have:
Increasing the resolution
In order to have a better accuracy in the estimation, we digitize now the shape at a higher resolution, i.e. with a smaller grid step. We choose as grid step h=0.1 instead of h=1:
Here is a picture of the contour:

At grid step 0.1, the estimation is better and close to the ground truth (165.961), since we get:
Length estimator comparison
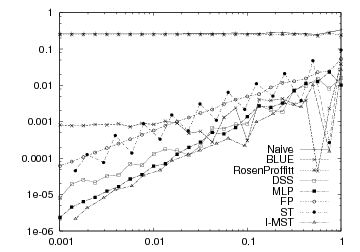
Many other length estimators are implemented (see L1LengthEstimator, BLUELocalLengthEstimator, RosenProffittLocalLengthEstimator, MLPLengthEstimator, FPLengthEstimator). You can compare them in a multiresolution framework thanks to the nice tool lengthEstimators.cpp. It provides a way of generating a given shape (whose parameters are given as arguments) at increasing resolution and list, for each resolution, the ground truth and the length estimated by all the available methods. For instance, the data of the following plot come from this tool:
Required includes
Here are the basic includes:
In order to generate an implicite or parametric shape, you need this:
To retrieve its contour, you should add:
And finally the length estimation requires: