Loading...
Searching...
No Matches
dec/exampleDiscreteExteriorCalculusSolve.cpp
Example of primal and dual Helmoltz decomposition in 2D and 3D using Discrete Exterior Calculus.
- See also
- Helmoltz decomposition
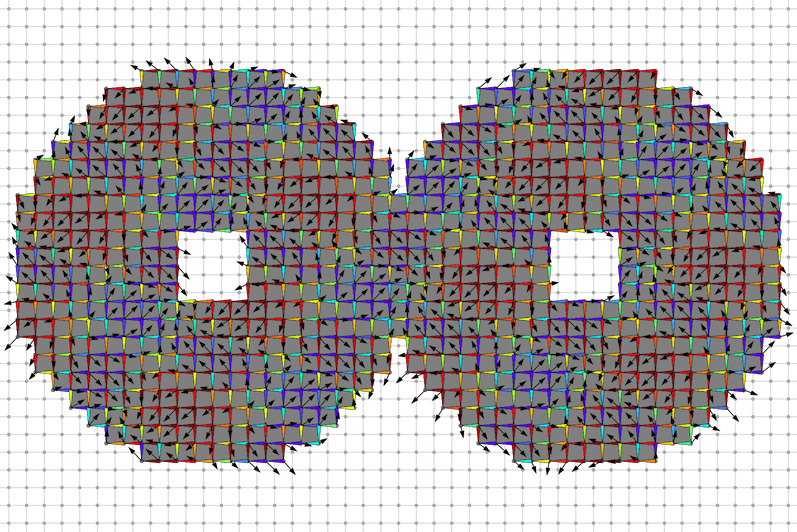 Primal Helmoltz decomposition harmonic component.
Primal Helmoltz decomposition harmonic component.
#include <string>
#include "DECExamplesCommon.h"
// always include EigenSupport.h before any other Eigen headers
#include "DGtal/math/linalg/EigenSupport.h"
#include "DGtal/dec/DiscreteExteriorCalculus.h"
#include "DGtal/dec/DiscreteExteriorCalculusSolver.h"
#include "DGtal/dec/DiscreteExteriorCalculusFactory.h"
#include "DGtal/io/viewers/PolyscopeViewer.h"
#include "DGtal/io/boards/Board2D.h"
#include "DGtal/io/readers/GenericReader.h"
using namespace DGtal;
using namespace std;
void solve2d_laplace()
{
// create discrete exterior calculus from set
trace.info() << "laplace = " << laplace << endl;
Calculus::DualForm0 dirac(calculus);
{
Board2D board;
board << domain;
board << dirac;
}
{ // simplicial llt
trace.beginBlock("simplicial llt");
Solver solver;
solver.compute(laplace);
Calculus::DualForm0 solution = solver.solve(dirac);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << solution << endl;
trace.endBlock();
Board2D board;
board << domain;
board << solution;
board.saveSVG("solve_laplace_simplicial_llt.svg");
}
{ // simplicial ldlt
trace.beginBlock("simplicial ldlt");
Solver solver;
solver.compute(laplace);
Calculus::DualForm0 solution = solver.solve(dirac);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << solution << endl;
trace.endBlock();
Board2D board;
board << domain;
board << solution;
board.saveSVG("solve_laplace_simplicial_ldlt.svg");
}
{ // conjugate gradient
trace.beginBlock("conjugate gradient");
Solver solver;
solver.compute(laplace);
Calculus::DualForm0 solution = solver.solve(dirac);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << solution << endl;
trace.endBlock();
Board2D board;
board << domain;
board << solution;
board.saveSVG("solve_laplace_conjugate_gradient.svg");
}
{ // biconjugate gradient stabilized
trace.beginBlock("biconjugate gradient stabilized (bicgstab)");
Solver solver;
solver.compute(laplace);
Calculus::DualForm0 solution = solver.solve(dirac);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << solution << endl;
trace.endBlock();
Board2D board;
board << domain;
board << solution;
board.saveSVG("solve_laplace_bicgstab.svg");
}
{ // sparselu
trace.beginBlock("sparse lu");
Solver solver;
solver.compute(laplace);
Calculus::DualForm0 solution = solver.solve(dirac);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << solution << endl;
trace.endBlock();
Board2D board;
board << domain;
board << solution;
board.saveSVG("solve_laplace_sparse_lu.svg");
}
{ // sparseqr
trace.beginBlock("sparse qr");
Solver solver;
solver.compute(-laplace);
Calculus::DualForm0 solution = -solver.solve(dirac);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << solution << endl;
trace.endBlock();
Board2D board;
board << domain;
board << solution;
board.saveSVG("solve_laplace_sparse_qr.svg");
}
trace.endBlock();
}
void solve2d_dual_decomposition()
{
trace.beginBlock("2d discrete exterior calculus solve dual helmoltz decomposition");
// create discrete exterior calculus from set
typedef DiscreteExteriorCalculus<2, 2, EigenLinearAlgebraBackend> Calculus;
typedef DiscreteExteriorCalculusFactory<EigenLinearAlgebraBackend> CalculusFactory;
// choose linear solver
typedef EigenLinearAlgebraBackend::SolverSparseQR LinearAlgebraSolver;
const LinearOperator<Calculus, 2, DUAL, 1, DUAL> ad2 = h1p * d0p * h2;
Calculus::DualVectorField input_vector_field(calculus);
for (Calculus::Index ii=0; ii<input_vector_field.length(); ii++)
{
const Z2i::RealPoint cell_center = Z2i::RealPoint(input_vector_field.getSCell(ii).preCell().coordinates)/2.;
input_vector_field.myCoordinates(ii, 0) = cos(-.5*cell_center[0]+ .3*cell_center[1]);
input_vector_field.myCoordinates(ii, 1) = cos(.4*cell_center[0]+ .8*cell_center[1]);
}
trace.info() << input_vector_field << endl;
const Calculus::DualForm1 input_one_form = calculus.flat(input_vector_field);
const Calculus::DualForm0 input_one_form_anti_derivated = ad1 * input_one_form;
const Calculus::DualForm2 input_one_form_derivated = d1 * input_one_form;
{
Board2D board;
board << domain;
board << calculus;
board << input_one_form;
board << input_vector_field;
board.saveSVG("solve_2d_dual_decomposition_calculus.svg");
}
Calculus::DualForm0 solution_curl_free(calculus);
{ // solve curl free problem
trace.beginBlock("solving curl free component");
Solver solver;
solver.compute(ad1 * d0);
solution_curl_free = solver.solve(input_one_form_anti_derivated);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << "min=" << solution_curl_free.myContainer.minCoeff() << " max=" << solution_curl_free.myContainer.maxCoeff() << endl;
trace.endBlock();
}
{
Board2D board;
board << domain;
board << calculus;
board << solution_curl_free;
board << calculus.sharp(d0*solution_curl_free);
board.saveSVG("solve_2d_dual_decomposition_curl_free.svg");
}
Calculus::DualForm2 solution_div_free(calculus);
{ // solve divergence free problem
trace.beginBlock("solving divergence free component");
Solver solver;
solver.compute(d1 * ad2);
solution_div_free = solver.solve(input_one_form_derivated);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << "min=" << solution_div_free.myContainer.minCoeff() << " max=" << solution_div_free.myContainer.maxCoeff() << endl;
trace.endBlock();
}
{
Board2D board;
board << domain;
board << calculus;
board << solution_div_free;
board << calculus.sharp(ad2*solution_div_free);
board.saveSVG("solve_2d_dual_decomposition_div_free.svg");
}
const Calculus::DualForm1 solution_harmonic = input_one_form - d0*solution_curl_free - ad2*solution_div_free;
trace.info() << "min=" << solution_harmonic.myContainer.minCoeff() << " max=" << solution_harmonic.myContainer.maxCoeff() << endl;
{
Board2D board;
board << domain;
board << calculus;
board << solution_harmonic;
board << calculus.sharp(solution_harmonic);
board.saveSVG("solve_2d_dual_decomposition_harmonic.svg");
}
trace.endBlock();
}
void solve2d_primal_decomposition()
{
trace.beginBlock("2d discrete exterior calculus solve primal helmoltz decomposition");
// create discrete exterior calculus from set
typedef DiscreteExteriorCalculus<2, 2, EigenLinearAlgebraBackend> Calculus;
typedef DiscreteExteriorCalculusFactory<EigenLinearAlgebraBackend> CalculusFactory;
// choose linear solver
typedef EigenLinearAlgebraBackend::SolverSparseQR LinearAlgebraSolver;
const LinearOperator<Calculus, 1, PRIMAL, 0, PRIMAL> ad1 = h2p * d1p * h1;
const LinearOperator<Calculus, 2, PRIMAL, 1, PRIMAL> ad2 = h1p * d0p * h2;
Calculus::PrimalVectorField input_vector_field(calculus);
for (Calculus::Index ii=0; ii<input_vector_field.length(); ii++)
{
const Z2i::RealPoint cell_center = Z2i::RealPoint(input_vector_field.getSCell(ii).preCell().coordinates)/2.;
input_vector_field.myCoordinates(ii, 0) = cos(-.5*cell_center[0]+ .3*cell_center[1]);
input_vector_field.myCoordinates(ii, 1) = cos(.4*cell_center[0]+ .8*cell_center[1]);
}
trace.info() << input_vector_field << endl;
const Calculus::PrimalForm1 input_one_form = calculus.flat(input_vector_field);
const Calculus::PrimalForm0 input_one_form_anti_derivated = ad1 * input_one_form;
const Calculus::PrimalForm2 input_one_form_derivated = d1 * input_one_form;
{
Board2D board;
board << domain;
board << calculus;
board << input_one_form;
board << input_vector_field;
board.saveSVG("solve_2d_primal_decomposition_calculus.svg");
}
Calculus::PrimalForm0 solution_curl_free(calculus);
{ // solve curl free problem
trace.beginBlock("solving curl free component");
Solver solver;
solver.compute(ad1 * d0);
solution_curl_free = solver.solve(input_one_form_anti_derivated);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << "min=" << solution_curl_free.myContainer.minCoeff() << " max=" << solution_curl_free.myContainer.maxCoeff() << endl;
trace.endBlock();
}
{
Board2D board;
board << domain;
board << calculus;
board << solution_curl_free;
board << calculus.sharp(d0*solution_curl_free);
board.saveSVG("solve_2d_primal_decomposition_curl_free.svg");
}
Calculus::PrimalForm2 solution_div_free(calculus);
{ // solve divergence free problem
trace.beginBlock("solving divergence free component");
Solver solver;
solver.compute(d1 * ad2);
solution_div_free = solver.solve(input_one_form_derivated);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << "min=" << solution_div_free.myContainer.minCoeff() << " max=" << solution_div_free.myContainer.maxCoeff() << endl;
trace.endBlock();
}
{
Board2D board;
board << domain;
board << calculus;
board << solution_div_free;
board << calculus.sharp(ad2*solution_div_free);
board.saveSVG("solve_2d_primal_decomposition_div_free.svg");
}
const Calculus::PrimalForm1 solution_harmonic = input_one_form - d0*solution_curl_free - ad2*solution_div_free;
trace.info() << "min=" << solution_harmonic.myContainer.minCoeff() << " max=" << solution_harmonic.myContainer.maxCoeff() << endl;
{
Board2D board;
board << domain;
board << calculus;
board << solution_harmonic;
board << calculus.sharp(solution_harmonic);
board.saveSVG("solve_2d_primal_decomposition_harmonic.svg");
}
trace.endBlock();
}
void solve3d_decomposition()
{
trace.beginBlock("3d discrete exterior calculus solve helmoltz decomposition");
// choose linear solver
typedef EigenLinearAlgebraBackend::SolverSparseQR LinearAlgebraSolver;
// create discrete exterior calculus from set
typedef DiscreteExteriorCalculus<3, 3, EigenLinearAlgebraBackend> Calculus;
Calculus calculus;
// outer ring
for (int kk=2; kk<=18; kk++)
for (int ll=4; ll<=36; ll++)
{
{ // bottom
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // top
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{ // left
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *calculus.myKSpace.uDirs(cell) == 2 ? Calculus::KSpace::NEG : Calculus::KSpace::POS );
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // right
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *calculus.myKSpace.uDirs(cell) == 2 ? Calculus::KSpace::POS : Calculus::KSpace::NEG );
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
}
// inner ring
for (int kk=2; kk<=18; kk++)
for (int ll=16; ll<=24; ll++)
{
{ // bottom
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *calculus.myKSpace.uDirs(cell) == 0 ? Calculus::KSpace::NEG : Calculus::KSpace::POS );
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{ // top
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = ( *calculus.myKSpace.uDirs(cell) == 0 ? Calculus::KSpace::POS : Calculus::KSpace::NEG );
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // left
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{ // right
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
}
// back and front
for (int kk=4; kk<=36; kk++)
for (int ll=0; ll<=12; ll++)
{
{ // back
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // front
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{ // back
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // front
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
}
// back and front
for (int kk=0; kk<=12; kk++)
for (int ll=16; ll<=24; ll++)
{
{ // back
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // front
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
{ // back
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::POS;
break;
case 2:
sign = Calculus::KSpace::NEG;
break;
default:
break;
}
}
{ // front
Calculus::KSpace::Sign sign = Calculus::KSpace::POS;
switch (dim)
{
case 0:
sign = Calculus::KSpace::POS;
break;
case 1:
sign = Calculus::KSpace::NEG;
break;
case 2:
sign = Calculus::KSpace::POS;
break;
default:
break;
}
}
}
calculus.updateIndexes();
{
typedef PolyscopeViewer<Z3i::Space, Z3i::KSpace> Viewer;
Viewer* viewer = new Viewer(calculus.myKSpace);
(*viewer) << DGtal::Color(255,0,0);
(*viewer) << domain;
(*viewer) << calculus;
viewer->show();
delete viewer;
}
const LinearOperator<Calculus, 1, PRIMAL, 0, PRIMAL> ad1 = h3p * d2p * h1;
const LinearOperator<Calculus, 2, PRIMAL, 1, PRIMAL> ad2 = h2p * d1p * h2;
{
const Eigen::VectorXd laplace_diag = laplace.myContainer.diagonal();
boost::array<int, 7> degrees;
std::fill(degrees.begin(), degrees.end(), 0);
for (int kk=0; kk<laplace_diag.rows(); kk++)
{
const int degree = laplace_diag[kk];
ASSERT( degree >= 0 );
ASSERT( static_cast<unsigned int>(degree) < degrees.size() );
degrees[degree] ++;
}
trace.info() << "node degrees" << endl;
for (int kk=0; kk<7; kk++)
trace.info() << kk << " " << degrees[kk] << endl;
}
Calculus::PrimalVectorField input_vector_field(calculus);
for (Calculus::Index ii=0; ii<input_vector_field.length(); ii++)
{
const Z3i::RealPoint cell_center = Z3i::RealPoint(input_vector_field.getSCell(ii).preCell().coordinates)/2.;
input_vector_field.myCoordinates(ii, 0) = -cos(-.3*cell_center[0] + .6*cell_center[1] + .8*cell_center[2]);
input_vector_field.myCoordinates(ii, 1) = sin(.8*cell_center[0] + .3*cell_center[1] - .4*cell_center[2]);
input_vector_field.myCoordinates(ii, 2) = -cos(cell_center[2]*.5);
}
trace.info() << input_vector_field << endl;
const Calculus::PrimalForm1 input_one_form = calculus.flat(input_vector_field);
const Calculus::PrimalForm0 input_one_form_anti_derivated = ad1 * input_one_form;
const Calculus::PrimalForm2 input_one_form_derivated = d1 * input_one_form;
{
typedef PolyscopeViewer<Z3i::Space, Z3i::KSpace> Viewer;
Viewer* viewer = new Viewer(calculus.myKSpace);
(*viewer) << input_one_form;
(*viewer) << input_one_form_derivated;
(*viewer) << input_one_form_anti_derivated;
(*viewer) << input_vector_field;
viewer->show();
delete viewer;
}
Calculus::PrimalForm0 solution_curl_free(calculus);
{ // solve curl free problem
trace.beginBlock("solving curl free component");
Solver solver;
solver.compute(ad1 * d0);
solution_curl_free = solver.solve(input_one_form_anti_derivated);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << "min=" << solution_curl_free.myContainer.minCoeff() << " max=" << solution_curl_free.myContainer.maxCoeff() << endl;
trace.endBlock();
}
{
typedef PolyscopeViewer<Z3i::Space, Z3i::KSpace> Viewer;
Viewer* viewer = new Viewer(calculus.myKSpace);
(*viewer) << solution_curl_free;
(*viewer) << calculus.sharp(d0*solution_curl_free);
viewer->show();
}
Calculus::PrimalForm2 solution_div_free(calculus);
{ // solve divergence free problem
trace.beginBlock("solving divergence free component");
Solver solver;
solver.compute(d1 * ad2);
solution_div_free = solver.solve(input_one_form_derivated);
trace.info() << solver.isValid() << " " << solver.myLinearAlgebraSolver.info() << endl;
trace.info() << "min=" << solution_div_free.myContainer.minCoeff() << " max=" << solution_div_free.myContainer.maxCoeff() << endl;
trace.endBlock();
}
{
typedef PolyscopeViewer<Z3i::Space, Z3i::KSpace> Viewer;
Viewer* viewer = new Viewer(calculus.myKSpace);
(*viewer) << solution_div_free;
(*viewer) << calculus.sharp(ad2*solution_div_free);
viewer->show();
}
const Calculus::PrimalForm1 solution_harmonic = input_one_form - d0*solution_curl_free - ad2*solution_div_free;
trace.info() << "min=" << solution_harmonic.myContainer.minCoeff() << " max=" << solution_harmonic.myContainer.maxCoeff() << endl;
{
typedef PolyscopeViewer<Z3i::Space, Z3i::KSpace> Viewer;
Viewer* viewer = new Viewer(calculus.myKSpace);
(*viewer) << solution_harmonic;
(*viewer) << calculus.sharp(solution_harmonic);
viewer->show();
}
trace.endBlock();
}
{
solve2d_laplace();
solve2d_dual_decomposition();
solve2d_primal_decomposition();
solve3d_decomposition();
return 0;
}
Aim: This class specializes a 'Board' class so as to display DGtal objects more naturally (with <<)....
Definition Board2D.h:71
Aim: This class provides static members to create DEC structures from various other DGtal structures.
Definition DiscreteExteriorCalculusFactory.h:62
Aim: This wraps a linear algebra solver around a discrete exterior calculus.
Definition DiscreteExteriorCalculusSolver.h:70
SolutionKForm solve(const InputKForm &input_kform) const
DiscreteExteriorCalculusSolver & compute(const Operator &linear_operator)
Aim: DiscreteExteriorCalculus represents a calculus in the dec package. This is the main structure in...
Definition DiscreteExteriorCalculus.h:98
Aim: LinearOperator represents discrete linear operator between discrete kforms in the DEC package.
Definition LinearOperator.h:69
void saveSVG(const char *filename, PageSize size=Board::BoundingBox, double margin=10.0) const
Definition Board.cpp:1011
DGtal is the top-level namespace which contains all DGtal functions and types.
Definition ClosedIntegerHalfPlane.h:49
Trace trace
STL namespace.
Definition Board2D.h:217
Eigen::SimplicialLLT< SparseMatrix > SolverSimplicialLLT
Solvers on sparse matrices.
Definition EigenSupport.h:105
Eigen::SimplicialLDLT< SparseMatrix > SolverSimplicialLDLT
Definition EigenSupport.h:106
Eigen::BiCGSTAB< SparseMatrix > SolverBiCGSTAB
Definition EigenSupport.h:108
Eigen::SparseQR< SparseMatrix, Eigen::COLAMDOrdering< SparseMatrix::Index > > SolverSparseQR
Definition EigenSupport.h:110
Eigen::SparseLU< SparseMatrix > SolverSparseLU
Definition EigenSupport.h:109
Eigen::ConjugateGradient< SparseMatrix > SolverConjugateGradient
Definition EigenSupport.h:107