Table of Contents
- Author(s) of this documentation:
- Pierre Gueth
Poisson equation
The Poisson equation can be written as:
\[ \Delta \phi = f \]
where \(\Delta\) is the Laplace operator, \(\phi\) the solution of the problem and \(f\) the input of the problem. The Poisson equation can be viewed as the heat equation when steady state is reached. \(f\) is then the constant spatial heating power applied to the structure and \(\phi\) is the temperature reached in steady state (up to a spatial constant). Here we choose \(f\) to be a Dirac delta function \(\delta\) to simulate a punctual heating on the structure.
Depending on border conditions, \(\Delta\) may have some null eigenvalues. In order to make it solvable, we use a regularized version of the Laplace operator \(\Delta_\mathrm{reg}\), defined below
\[ \Delta_\mathrm{reg} = \Delta + \lambda I \]
where \(I\) is the identity operator and \(\lambda\) is the regularization scalar, chosen small with respect to \(\Delta\) eigenvalues. Linear regularized solution are the same solution as least square problem solution of the non regularized problem. \(I\) is generated using DiscreteExteriorCalculus.identity.
One can use the general Laplace operator definition.
\[ \Delta = \star d \star d = \delta d \]
However, for convenience DiscreteExteriorCalculus provides a method to get the Laplace operator directly.
1D Poisson resolution
In this example, we create an 1D linear structure embedded in a 2D space and we solve a non regularized Poisson equation on this structure.
Boundary conditions effect are illustrated for the two classical boundary conditions.
- Neumann boundary condition forces the derivative to be null along the border of the structure. Here, this means that heat can't flow out the start and the end of the linear structure.
- Dirichlet boundary condition connects borders of the structure to null potential. With our heat analogy, this means that the start and the end of the linear structure are connected to thermostat, which are given the null temperature.
Boundary conditions are changed from Neumann to Dirichlet conditions by adding dangling 1-cells at the beginning and at the end of the structure. Snippets are taken from testLinearStructure.cpp.
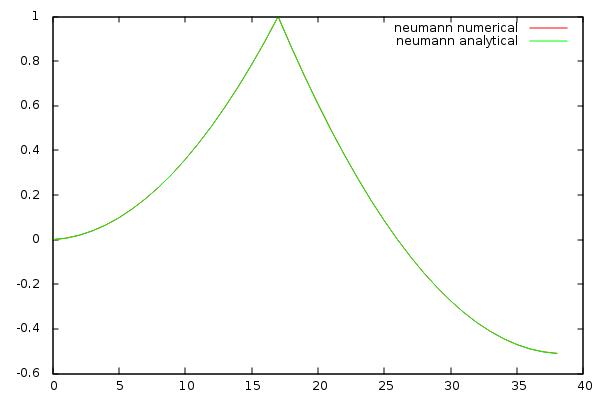
Neumann boundary condition
First, an empty calculus structure is created and, using simple for loops, it is filled with some 0-cells and 1-cells to from a linear structure. When filled manually with DiscreteExteriorCalculus.insertSCell, one can pass the primal and dual sizes of each cell which default to 1. Temperature nodes are associated primal 0-cells. Note that to enforce Neumann boundary conditions, the linear structure has to end with 0-cells. Moreover some 1-cells are inserted as negative cells to match their orientation with the orientation of the linear structure.
The input heat vector \(f\), which is a primal 0-form in the DEC formulation, is then created and is given values of a Dirac pulse shifted at the right position.

The primal non regularized Laplace operator \(\Delta\) is generated using DiscreteExteriorCalculus.laplace. The primal exterior derivative from 0-form to 1-form will be used to compute the gradient solution.
Now the problem is fully defined and there one thing left to do: solving it. The resolution is done by DiscreteExteriorCalculusSolver. This class takes the actual linear solver used as the second template parameter. Any class that validates the CLinearAlgebraSolver concept can be wrapped by DiscreteExteriorCalculusSolver. If DGtal was compiled with eigen support enabled as described in DEC linear solver, some solvers will be available in the EigenLinearAlgebraBackend. Here, we will use the EigenLinearAlgebraBackend::SolverSparseQR solver. Once created the solver is given the operator using DiscreteExteriorCalculusSolver.compute. The input dirac 0-form is passed to DiscreteExteriorCalculusSolver.solve, which return the solution of the problem.
Since the dirac input is null everywhere except at a single point, this means that the second derivative of the solution is null everywhere except at the dirac position. An analytic form can be expressed as a continuous piece-wise quadratic function. Numerical values of the solution fit analytic values with at least a relative precision of 1e-5.


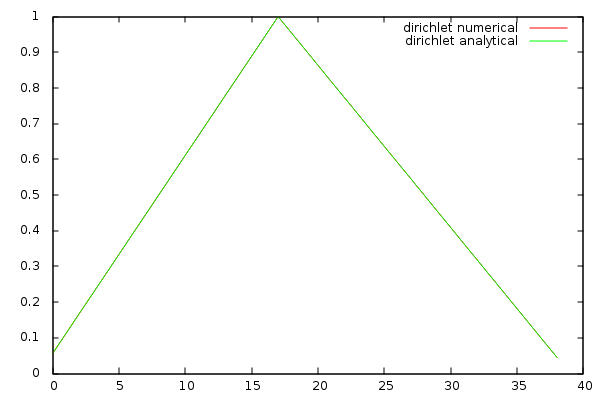
Dirichlet boundary condition
Dirichlet boundary condition fixes value of 0-forms to zero along borders of the structure. Two dangling 1-cells are added at each end of the Neumann structure to switch to Dirichlet boundary condition. Since those 1-cells are not connected to a 0-cell on one of their border, this will simulate the presence of zero-valued 0-cell in those places through enforcing Dirichlet boundary conditions.
The input Dirac can be used as in the Neumann case since no 0-cells has been added to the structure.

Laplace operator needs to be rebuild, even if the code doesn't change.
Solving the problem is achieved by using the same code as for the Neumann case. This time the analytic solution is piece-wise linear and take a constant null value at the border of the structure, as expect from the Dirichlet boundary condition.
Numerical values of the solution fit analytic values with at least a relative precision of 1e-5.


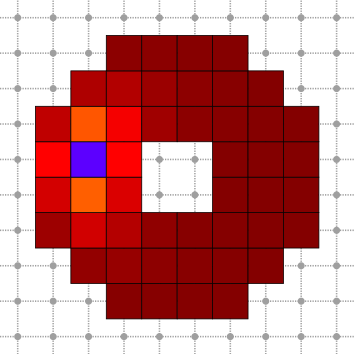
2D Poisson problem
In this example, we create a 2D ring structure and we solve a regularized Poisson equation on this structure. Snippets are taken from exampleDiscreteExteriorCalculusSolve.cpp. First the structure is created from a digital set.
Then we compute the dual regularized Laplace operator with \(\lambda = 0.01 \).
Input k-form \(y\) is a Dirac delta positioned on the dual 0-cell at coordinates \((2,5)\). DiscreteExteriorCalculus.getIndex return the index of the dual 0-form container associated with the dirac position cell.
The following illustration represents the dual of the input. Hence, since we have specified a dirac on "dual 0-cell", its primal representation attaches information to (primal) 2-cells.

We try to solve the problem using EigenLinearAlgebraBackend::SolverSimplicialLLT, but DiscreteExteriorCalculusSolver.isValid reports an error. Underlying linear algebra solver DiscreteExteriorCalculusSolver.solver.info reports a numerical_error.

Since the first solver failed, let's use another one: EigenLinearAlgebraBackend::SolverSimplicialLDLT for example. This time DiscreteExteriorCalculusSolver.isValid is true after computing problem solution and the solution dual 0-form contains the solution of the problem.
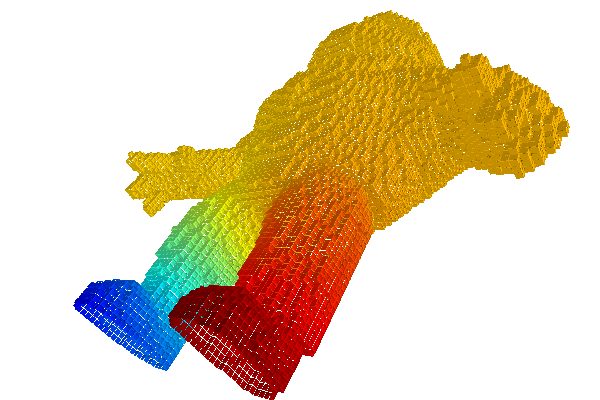
Embedded 2D Poisson problem
In this example, we create an embedded 2D structure from a DigitalSurface and we solve a dual Poisson equation with Neumann boundaries condition. Snippets are taken from exampleDECSurface.cpp.
First we load the Alcapone image and extract its boundary surface. Note that the Khalimsky space domain opens the surface under the feet of Alcapone.
The DEC structure is then create using DiscreteExteriorCalculusFactory::createFromNSCells. Borders are not added to the structure.

Dual 0-form \(\rho\) is the input of the Poisson problem. Left foot has positive value and right foot has negative value.
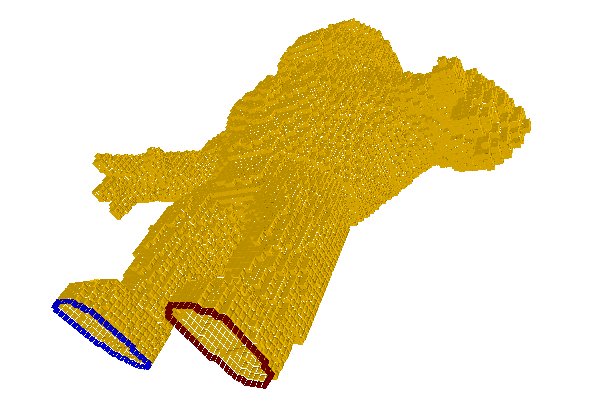
Dual Laplace operator is computed and passed to the solver using DiscreteExteriorCalculusSolver.compute. The dual 0-form solution \(\phi\) is returned by DiscreteExteriorCalculusSolver.solve.