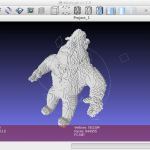
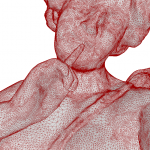
Digital Surface Regularization
Eigenvectors of the digital Laplace-Beltrami operator.
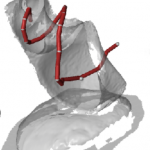
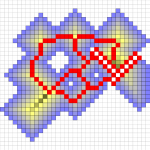
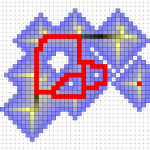
Illustration of centerline extraction using accumulation and confidence map.

Illustration of centerline extraction using accumulation and confidence map.
Tangential cover with alpha-thick segments with alpha = 4
Kanungo noise model on 3D dataset.

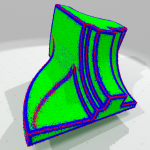
Feature selection on a noisy Fandisk, using Integral Invariant Curvature Estimator. Red: feature, Blue: smooth part, Green: flat part
Snapshot of an example of viewer3DImage-8Image3D on Raspberry Pi 2 (raspbian jessie)
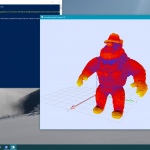
Example of Integral Invariant Curvature3D on Windows10

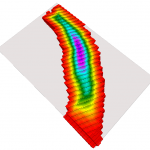
Mean curvature on “dragon” shape
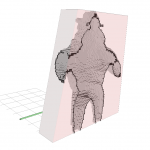
Mean curvature on Armadillo

Mean curvature on lucy
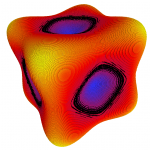
Mean curvature on a noisy octa-flower
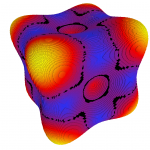
Mean curvature on a octa-flower shape

Mean curvature (integral invariant) on a bunny shape.
Another rendering of OBJ file given by vol2obj tool.
Rendering of digital bunny (using vol2obj tool + blender)

Example of rendering from OBJ export of a curvature map.
Example of wood display with Viewer3D and quad mesh embedding in 3D volumetric scan of wood.
Example of wood display with Viewer3D and quad mesh embedding in 3D volumetric scan of wood.

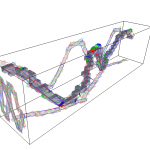
3D curve
A view of a 3D curve with its tangential cover and projections (see DGtalTools/visualisation/3dCurveViewer)
L_p separable metrics which can be used in DGtal volumetric tools (from left to right, top to bottom, p={1,2,4,0.8,1.3,43.2}.
Gaussian curvature using Integral Invariants (with zero curvature surfels in black).

Mean curvature using Integral Invariants (with zero curvature surfels in black).
Voronoi diagram map in dimension 2 for a random set of sites
Voronoi diagram map in 2d for a random set of sites (on color per digital voronoi cell)

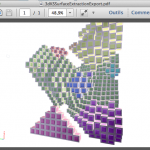
Export from Display3D to OFF allowing to generate a U3D/PDF format
Example of OFF generation from a Display3D object.
Importing 3D Mesh in Display3D viewers

Simple point table for topology (8,4)
Simple point table for topology (8,4).
Simple point table for topology (4,8)
Simple point table for topology (4,8).
Comparison between two convolution kernels (constant convolution kernel and Gaussian Kernel)

Normal vector estimation based on a convolution kernel on elementary normal vector based on a convolution kernel on elementary normal vector
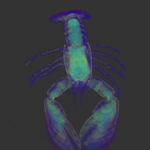
Marching-cubes surface of lobster.vol at isovalue 40
Marching-cubes surface of lobster.vol at isovalue 40
Implicit polynomial surface
Extraction of implicit polynomial surface “3*x^2-2*y^2+z^3+5y^2*(z-1)*(z+1)”

Surface (x^2+y^2+2z^2-1)*(z^2x-0.1)=0
Extraction of surface defined by some implicit polynomial.
Implicit surface "Miau"
Extraction of implicit polynomial surface “Miau”.
Surface of implicit polynomial "durchblick"
Extraction of surface “durchblick” defined by some implicit polynomial.

Surface of polynomial "crixxi"
Extraction of surface “crixxi” defined by some implicit polynomial.
Intersection of two balls
Boundary and frontiers in a labelled image.
cat10 image
Marching-cube surface or triangulation of digital surface “cat10.vol”.

lobster image
Breadth-first traversal onto the “lobster” digital surface.
Saturated decomposition of a digital curve inti digital circular arcs.
Distance map from a knot withing a wood beam

DGtal used in a software of 3D branch measurements
Extraction of connected Signed Khalimsky Cell from DGtalSet
Tracking 2D surfel boundary from single surfel Cell of 3D Khalimsky Space
Tracking 2D surfel boundary from single surfel Cell of 3D Khalimsky Space

Displaying Khalimsky Signed Cells in 3D
Displaying Khalimsky Signed Cells in 3D
Displaying Khalimsky Cells in 3D
Displaying Khalimsky Cells in 3D

2D contour extraction in the Khalimsky cellular model.
Visualisation of 3D object border with ClippingPlane objects
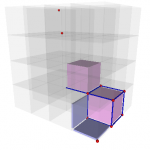
Display of 18-6 adjacency from two 18-6 objects

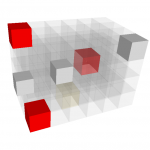
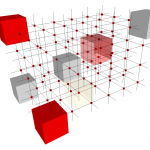
3D Domain visualization with three digital sets
3D Domain visualization with some elements (domain displayed in “Paving” mode)
3D Domain visualization with some elements (domain displayed in “Grid” mode)

3D Domain visualization with two digital sets
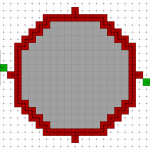
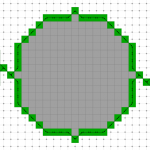
3D homotopic shape thinning in the (6,26)-adjacency.
Distance Transformation using the Euclidean distance using a random set of seeds.

Distance Transformation in 3D using the Manhattan distance (l_1).
Distance Transformation using the Euclidean distance
3D Distance transformation using the chessboard (l_infinity) distance.

3D volume visualization
Example of the decomposition of a simple 4-connected curve into maximal Discrete Straight Segments (greedy algorithm).
Decomposition of a contour into standard Discrete Straight Segments using a greedy process.

Visualisation of some iso contours
Contour visualization with original source image
Distance Transformation using the Euclidean distance using a random set of seeds.

Distance Transformation in 2D using the Manhattan distance (l_1).
Distance Transformation using the Chessboard (l_infinity) distance.
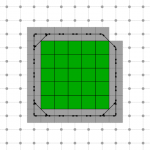
2D homotopic shape thinning in the (8,4)-adjacency

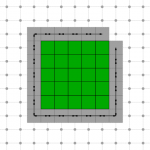
2D homotopic shape thinning in (4,8)-topology
Examples of colormaps available in the DGtalBoard system.
Implicit function representation on a classical ImageContainer.

Implicit domain representation using a Pointerless QuadTree (a.k.a. HashTree in n-D).
Filling of a 2D domain with (8,8)-adjacency.
Filling of a 2D domain with (8,4)-adjacency.

Filling of a 2D domain with (4,8)-adjacency.
Filling of a 2D domain with (4,4)-adjacency.
Border tracking and labelling using the 4-adjacency.

Border tracking and labelling using the 8-adjacency.