Propagation equation

Propagation plays a important role in physics as it models a lot a problem ranging from classical oscillators to electromagnetism, relativistic gravitation and quantum mechanics. Here we will study the linear propagation equation of a time dependent scalar wave function \(\psi(x,t)\), modelled as dual 0-form in the DEC framework,

\[ \Delta \psi + \frac{1}{c^2} \frac{\partial^2\psi}{\partial t^2} = \left( \Delta + \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \right) \psi = \rho \]

where \(c\) is propagation speed inside the medium and \(\rho(x,t)\) is the scalar concentration field that generates waves. The \(+\) differs from the classical physics equation since here we consider \(\Delta\) to have positive eigenvalues, which is the opposite of the definition of the Laplace operator in physics. As DEC handles only spatial dimensions, we will present two classical tricks that can be used to handle the time dependent in many physics problems. For simplicity of notation, we define the propagation operator \(\square\).

\[ \square = \Delta + \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \]

Temporal resolution with initial condition

In this example, we compute the time evolution of a wave given the initial (potentially complex) wave function \(\psi(x,0)=\psi_0(x)\). Snippets are taken from examplePropagation.cpp.

Consider the homogeneous propagation equation, where \(\rho(x,t) = 0\),

\[ \square \psi = 0 \]

The Laplace operator \(\Delta\) is computed using DiscreteExteriorCalculus.laplace. Note that the problem is expressed on the dual structure. A small fraction of DiscreteExteriorCalculus.identity is added to ensure a proper definition of \(\Delta\).

const Calculus::DualIdentity0 laplace = calculus.laplace<DUAL>() + 1e-8 * calculus.identity<0, DUAL>();

DGtal::DUAL

@ DUAL

Definition: Duality.h:62

Since \(\Delta\) is a positive semi definite real valued Hermitian operator, its eigenvalues are real and positive and its eigenvectors are real.

\[ \Delta \phi_i = k_i^2 \, \phi_i \]

where \(\phi_i\) are eigenvectors and \(k_i^2\) are corresponding eigenvalues. Eigen pairs can be computed using Eigen::SelfAdjointEigenSolver for small system; \(\phi_i\) is then the ith column of the eigen_vectors matrix. For larger systems, one can use more advance techniques such as band shift invert resolution.

        typedef Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> EigenSolverMatrix;
        const EigenSolverMatrix eigen_solver(laplace.myContainer);
 
        const Eigen::VectorXd eigen_values = eigen_solver.eigenvalues();
        const Eigen::MatrixXd eigen_vectors = eigen_solver.eigenvectors();

\(\phi_i\) form an orthonormal basis of the Laplace operator solutions. One can use this property to define \(\psi_i\) an orthonormal basis of solutions of the homogeneous propagation equation (it is easy to check that \(\square \psi_i = 0\)).

\[ \psi_i(x,t) = \phi_k(x) \, e^{j c k_i t} \]

where \(j\) is the imaginary unit. One can project any solution \(\psi\) of the propagation equation onto this basis. The (potentially complex) coordinates \(p_i\) of \(\psi\) in the \(\psi_i\) basis are

\[ p_i = \left< \psi | \psi_i \right> \]

where, for all \(t\), \(\left< \bullet | \bullet \right> \) is the inner product between dual 0-forms. In the DEC framework, such a product can be computed as the scalar product between the discrete value vector KForm.myContainer. We can then write \(\psi\) as a linear combination of \(\psi_i\)

\[ \psi = p_i \, \psi_i \]

where the summation over \(i\) is implicit. Note that for \(t=0\), \(\psi_i(x,0) = \phi_i(x)\). To solve the temporal evolution from \(\psi_0(x)\), all we need to do is to find its initial projections \(p_{0i}\) and let complex exponentials do the their duty to predict future (and past) wave functions.

\[ p_{0i} = \left< \psi_0 | \phi_i \right> \]

Those inner product are computed by multiplying the initial wave 0-form container with the transposed eigen_vectors matrix.

Eigen::VectorXcd initial_projections = eigen_vectors.transpose() * initial_wave;

For aesthetic reason, initial projections are filtered to keep only low frequency (high wavelength) components.

        const Calculus::Scalar lambda_cutoff = 4.5;
        const Calculus::Scalar angular_frequency_cutoff = 2*M_PI * cc / lambda_cutoff;
        int cutted = 0;
        for (int kk=0; kk<initial_projections.rows(); kk++)
        {
            const Calculus::Scalar angular_frequency = angular_frequencies(kk);
            if (angular_frequency < angular_frequency_cutoff) continue;
            initial_projections(kk) = 0;
            cutted ++;
        }

To get the wave function for any other time \(t\), \(\psi\) is computed as

\[ \psi(x,t) = p_{0i} \, \psi_i(x,t) = p_{0i} \, \phi_i(x) \, e^{j c k_i t} \]

This translate to the following code where the term \(c k_i\) is precomputed for all times.

const Eigen::VectorXd angular_frequencies = cc * eigen_values.array().sqrt();

            const Calculus::Scalar time = kk/20.;
            const Eigen::VectorXcd current_projections = (angular_frequencies * std::complex<double>(0,time)).array().exp() * initial_projections.array();
            const Eigen::VectorXcd current_wave = eigen_vectors * current_projections;

For real wave functions, knowing the initial wave is not enough the get a unique answer. One would have to know temporal initial wave derivative as well to fully determine the propagation behavior. When one use complex wave functions, the derivative initial conditions are replaced by the phase of the initial wave. By changing the phase field, one would get different behavior. For example if one choose initial wave as described above, one would get a nice uniform propagation of the wave.

    for (int xx=9; xx<13; xx++)
    for (int yy=13; yy<17; yy++)
    {
        const Point point(xx,yy);
        const Cell cell = calculus.myKSpace.uSpel(point);
        const Index index = calculus.getCellIndex(cell);
        initial_wave(index) = 1;
    }

Real part of wave propagating from initial conditions with null phase.

If, on the other hand, one starts to mess with the phase on the initial wave and introduce phase variation along y, one would get a directional propagation of the wave along -y.

    for (int xx=9; xx<13; xx++)
    for (int yy=13; yy<17; yy++)
    {
        const Point point(xx,yy);
        const Cell cell = calculus.myKSpace.uSpel(point);
        const Index index = calculus.getCellIndex(cell);
        initial_wave(index) = std::exp(std::complex<double>(0,2*M_PI*(yy-14.5)/8));
    }

Real part of wave propagating from initial conditions with phase variation along y.

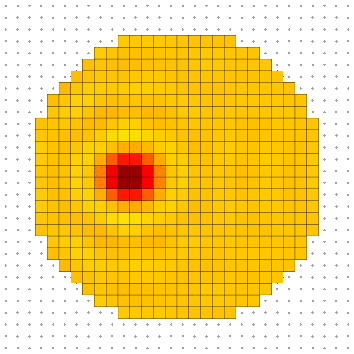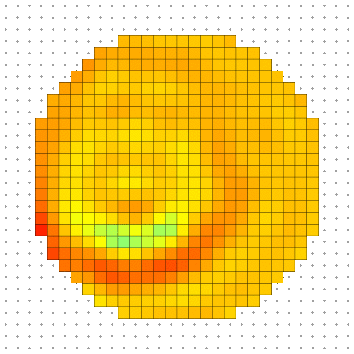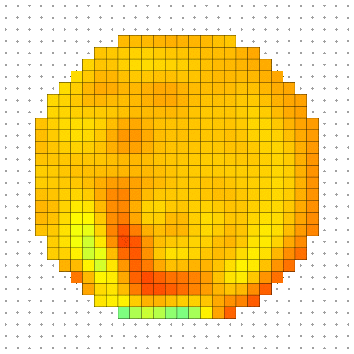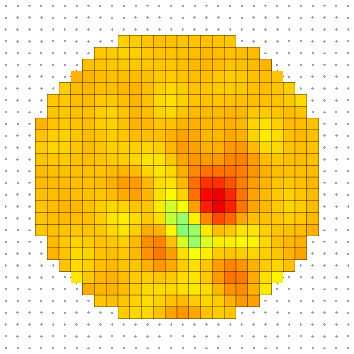
Established permanent regime solution

In this section, we compute the established standing wave generated by a standing concentration field oscillating at a single angular frequency \(\omega_p\). One can define the wavenumber \(k_p = \frac{\omega_p}{c}\) and the wavelength \(\lambda_p = \frac{2 \pi c}{\omega_p}\) equivalently to \(\omega_p\). The established standing wave hypothesis induce a separability of spatial and temporal components: \(\rho(x,t)\) can be expressed as the product between \(\rho_p(x)\), the spatial part, and \(e^{j \omega_p t}\), the temporal part.

\[ \rho(x,t) = \rho_p(x) \, e^{j \omega_p t} = \rho_p(x) \, e^{j c k_p t} = \rho_p(x) \, e^{\frac{2 \pi c t}{\lambda_p}} \]

The separability applies to \(\psi(x,t)\) too. This linearity of \(\square\) implies that the solution is vibrating at the same frequency as the excitation.

\[ \psi(x,t) = \psi_p(x) \, e^{j c k_p t} \]

The propagation operator gives a relation between \(\psi_p\) and \(\rho_p\) through the \((\Delta - k_p^2 I)\) operator.

\[ \square \psi = \rho \;\Leftrightarrow\; ( \Delta - k_p^2 \, I ) \, \psi_p = \rho_p \;\Leftrightarrow\; \psi_p = ( \Delta - k_p^2 \, I )^{-1} \, \rho_p \]

where \(I\) is the identity operator on dual 0-forms and \(( \Delta - k_p^2 I )^{-1}\) is the inverse of \(( \Delta - k_p^2 I )\), always uniquely defined. If \((\phi_i, k_{\Delta i}^2)\) are eigen pairs of \(\Delta\),

\[ \Delta \phi_i = k_{\Delta i}^2 \, \phi_i \]

it is easy to show that \((\phi_i, \frac{1}{k_{\Delta i}^2 - k_p^2})\) are eigen pairs of \((\Delta - k_p^2 I)^{-1}\). Eigenvectors stay the same, only eigenvalues are changed.

\[ ( \Delta - k_p^2 \, I )^{-1} \phi_i = \frac{1}{k_{\Delta i}^2-k_p^2} \, \phi_i \]

Using \(p_{pi}\) and \(r_{pi}\), the coordinates of \(\psi_p\) and \(\rho_p\) in the \(\phi_i\) basis, defined as

\[ p_{pi} = \left< \psi_p | \phi_i \right> \; r_{pi} = \left<\rho_p | \phi_i \right> \]

the solution of the problem is the computed as

\[ p_{pi} = \frac{r_{pi}}{k_{\Delta i}^2 - k_p^2} \]

This leads to the following definition for \(( \Delta - k_p^2 I )^{-1}\), as concentration_to_wave, in the DEC framework.

const Eigen::VectorXd dalembert_eigen_values = (laplace_eigen_values.array() - (2*M_PI/lambda)*(2*M_PI/lambda)).array().inverse();

const Eigen::MatrixXd concentration_to_wave = laplace_eigen_vectors * dalembert_eigen_values.asDiagonal() * laplace_eigen_vectors.transpose();

The spatial part of the established wave is computed by applying concentration_to_wave to the concentration 0-form container.

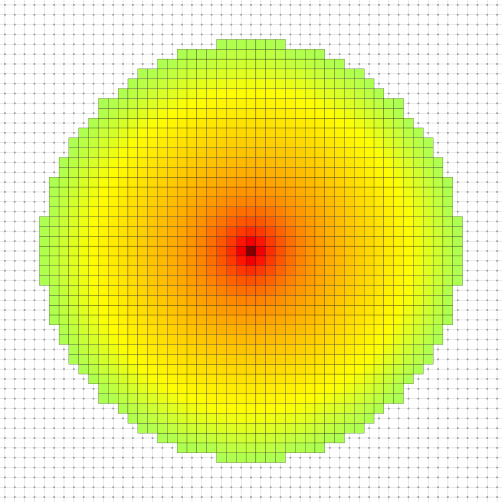
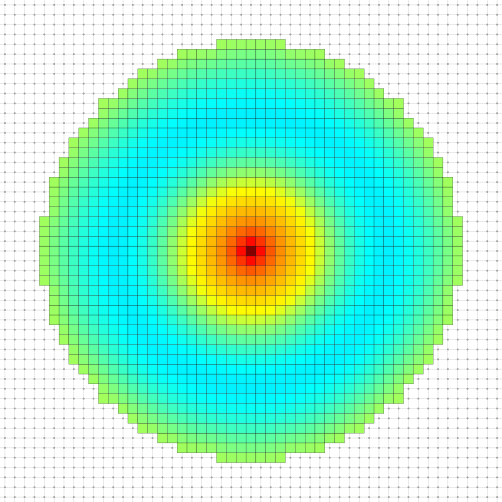
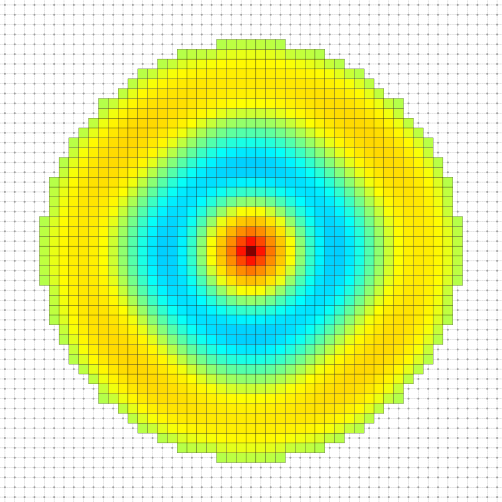
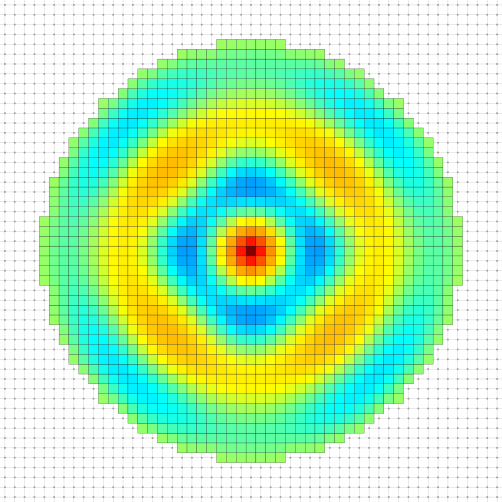
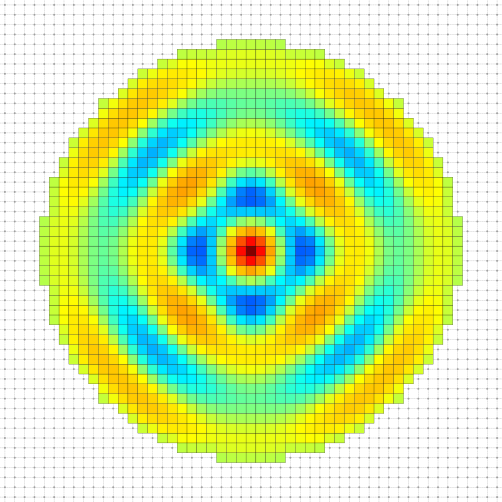
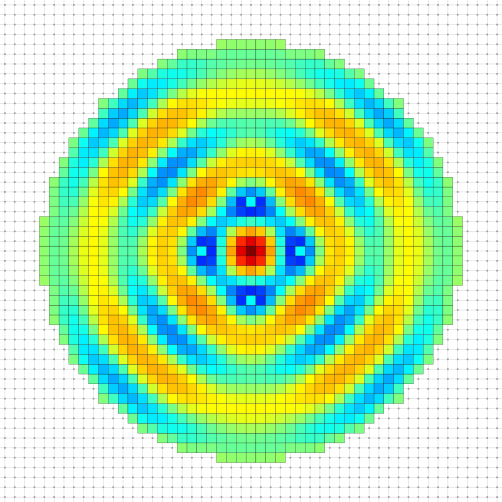
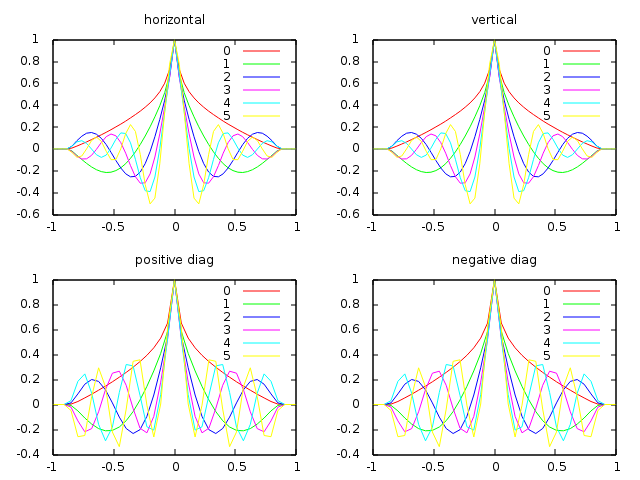
Calculus::DualForm0 wave(calculus, concentration_to_wave * concentration.myContainer);

To illustrate this section, we compute the established standing waves on a disk with a punctual excitation at its center for multiple wavelength \(\lambda_{pk}\) such that a standing wave with \(k\) extremums between center and border is created.

\[ r = k \frac{\lambda_{pk}}{2} + \frac{\lambda_{pk}}{4} \]

where \(r\) is the radius of the disk. Here we took \(r = 20.75 \mathrm{px}\).

const Calculus::Scalar lambda = 4*20.75/(1+2*ll);