Table of Contents
- Date
- 2012/12/05
Overview
The concept of point functor describes a mapping between the points of a digital space and a set of values. The only method of a point functor is the operator(), which must take a point as argument and must return a value.
The concept of constant image is a point functor bounded by a domain. It is thus a refinement of the concept of point functor, describing a mapping between points and values, but having in addition a domain, returned by the domain method, and a range of values (for each point of the domain), returned by the constRange method.
The concept of image, which is a refinement of the concept of constant image, provides extra services to update values.
Any model of image must have a method setValue taking a point and a value as input parameters and updating the value associated with the given point with the given value.
In addition, they must have a range, returned by the range method, providing output iterators.
Different models of images are available: ImageContainerBySTLVector, ImageContainerBySTLMap, ImageContainerByITKImage (a wrapper for ITK images) and — coming soon — experimental::ImageContainerByHashTree.
Let us go into details
In this section, the concepts and the main services to read and write values in images are detailed.
Concepts
Any model of the concept concepts::CPointFunctor must have two nested types:
- Point, which specifies the type for a point.
- Value, which specifies the type for a value.
Moreover, it must have the following method:
operator(), which takes a point as argument and returns a value, like a function.
The concept concepts::CConstImage is a refinement of concepts::CPointFunctor. Its models must have two extra nested types:
- Domain, a model of concepts::CDomain
- ConstRange, a model of concepts::CConstBidirectionalRangeFromPoint
Obviously, there are two methods that return instances of these two types:
domain, which returns a constant reference on the image domainconstRange, which returns a range providing constant bidirectional iterators on the image values (associated to each point of the image domain)
You can see Digital Spaces, Points, Vectors and Domains for more details about spaces and domains and Ranges of values for more details about ranges in images.
The concept concepts::CImage is a refinement of concepts::CConstImage.
Images, instead of constant ones, provide services to update values. The main way of assigning values to points is the following method:
setValue, which updates a given value at a given point.
Moreover, in addition to the ConstRange, images must have the following inner type:
- Range, a model of concepts::CConstBidirectionalRangeFromPoint, like ConstRange, and a model of concepts::CBidirectionalRangeWithWritableIteratorFromPoint, which must provide output iterators for incrementally updating a (sub)range of values.
Obviously, you can get an instance of this type using the following method:
range, which returns a range providing both constant bidirectional iterators and output iterators.
Lastly, note that the Value type in the (constant) images is expected to be at least a model of concepts::CLabel, ie.
to be default-constructible, assignable and equality comparable.
- Note
- In the snippets of the following subsections, the type of image used is
Imageand its instances areimage,image1,image2.
Main methods
All models of images have a domain returned by the method domain. This domain is the set of points for which the image is defined and has values. Since a domain is a range, you can straightforwardly use it in order to iterate over the points of an image.
Models of images have also two main methods in order to read or write values at a given point:
operator()to get the value associated to a given pointsetValueto assign a value to a given point.
Note that this method of iterating over the values of an image is not always the fastest and that is why we also provide ranges of values.
Ranges of values
Constant images provide a constant range of values returned by the constRange method. As every model of concepts::CConstBidirectionalRange, it provides begin, end, rbegin and rend methods returning constant iterators to iterate over the values in the forward or backward direction.
However, this range is also a model of concepts::CConstBidirectionalRangeFromPoint, which is a refinement of concepts::CConstBidirectionalRange. That is why it also has overloaded versions of the begin and rbegin methods taking a point as input argument. This provides a way of iterating on sub-ranges defined from points.
Note that if the point does not belong to the domain, the returned iterators (resp. reverse iterators) must be equal to the end (resp. rend) methods.
Images provide in addition to a constant range, a richer range returned by the range method. This range is not only a model of concepts::CBidirectionalRangeFromPoint, but also a model of concepts::CBidirectionalRangeWithWritableIteratorFromPoint. That is why, it must have two methods:
outputIterator and routputIterator returning output iterators. Moreover, it must have overloaded versions of these methods taking a point as input argument. Thus, these output iterators are useful in order to incrementaly fill (a part of) an image. For instance, you can fill an image from the values of another one (assumed to have the same domain) as follows:
Main models
Different models of images are available: ImageContainerBySTLVector, ImageContainerBySTLMap, experimental::ImageContainerByHashTree and ImageContainerByITKImage, a wrapper for ITK images.
ImageContainerBySTLVector
ImageContainerBySTLVector is a model of concepts::CImage that inherits the STL vector class. The hyper-rectangular domain, which the only model of domain accepted, is linearized so that
each point is mapped, from its coordinates, into an index and each index is mapped into a unique value, as in any one-dimensional array.
Let \( n \) be the domain size (the number of points). At construction all the needed space is allocated and filled with a default value (0) in \( O(n) \) space and time. After that, you can access to the value associated to any point at any time. Each access for reading (operator()) or writing ('setValue`) values is in \( O(1) \).
The (constant) range of this class only used the built-in iterators of the underlying STL vector. It is therefore a fast way of iterating over the values of the image.
ImageContainerBySTLMap
ImageContainerBySTLMap is a model of concepts::CImage that inherits the STL map class. The domain can be any set of points. Values are stored and associated to points in pairs point-value. The set of points stored in this way may be any domain subset. A default value (user-defined) is automatically associated to each point of the domain that does not belong the subset for which values are known. Once constructed (in \( O(1) \)), the image is valid and every point of the image domain has a value, which can be read and overwritten.
The pairs point-value are stored in a red-black tree, where the points are used as keys, so that
each access for reading (operator()) or writing (setValue) values is in \( O(log m) \), where \( m \) is the cardinal of the subset for which values are known (less or equal to the domain size \( n \)).
The (constant) range of this class adapts the domain iterators in order to deal with values instead of points. The operator* of the iterators provided by the range calls the operator() and use the setValue method of the class.
ImageContainerByHashTree
experimental::ImageContainerByHashTree is an experimental image container implementing a pointerless nD-tree structure. In dimension 2 and 3, this structure is similar to quadtree and octree repsectively in which hierarchical links between a node and its children is given by prefix of a binary representation of the node coordinates using Morton keys. Finally, data values are stored in the structure in a hash table whose hash function is a suffix on the Morton key code.
Such container is well adapted for high resolution sparse images.
For more details, please refer to [81]
Image Adapter classes
ImageAdapter, ConstImageAdapter are perfect swiss-knifes to transform and adapt images (change their domain definition, change their value types, ...). These classses are parametrized by several types and functor in order to adapt the behavior of image getters/setters (operator() and setValue methods). These adapted behaviors are computed on-the-fly when calling these methods.
ConstImageAdapter requires several types and functors to create a "read-only" adapted image (operator(), constRange(), ...)
ImageAdapter requires a supplementary functor and allows write access to the image (setValue methods, range(), ... )
- Note
- Functors used to convert domains or values may be complex. Keep in mind that each time operator() or setValue() methods are called, such functors are evaluated (with potential side-effects depending on the functors).
In addition, ArrayImageAdapter allows to convert any iterable storage (like a C-style array or some DGtal image models), to a concepts::CImage (or concepts::CConstImage) model with the possibility to restrict his visibility to a sub-domain of the definition domain.
ConstImageAdapter
ConstImageAdapter is a small class that adapts any (constant or not) image into a constant one, which provides a virtual view (so read-only) of the true values contained in the adapted image. The class is parametrized by several template arguments: TImageContainer: the type of image to adapt. TNewDomain: the type of the new domain. TFunctorD: type of functor used to convert image domain points to new domain points TNewValue: type of the new image value type. TFucntorV: functor to convert values.
The values associated to access the point values are adapted
with a functor g and a functor f given at construction so that operator() calls f(img(g(aPoint))), instead of calling directly img.operator() of the underlying image img.
Functor g (and/or functor f) can be a default functor, i.e. a simple functor that just returns its argument.
In order to illustrate the next ConstImageAdapter usage samples, we are going a) to use these includes:
b) then define these types and variables:
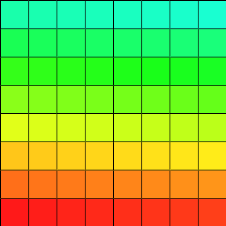
c) then define a simple 16x16 (1,1) to (16,16) image (of 'unsigned char' type):
filled with 0 to 255 values like that:
which looks like that with a simple HueShadeColorMap varying from 0 to 255 and with (1,1) the first bottom-left point:

Here is now the construction of a simple image adapter that use a subdomain of the initial image domain to access the first bottom-left 8x8 image:
and here is the result:
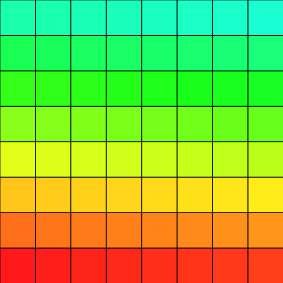
Here is then the construction of an image adapter that use a specific domain: here, only one pixel on two in x and y coordinates, created like that:
from the initial image domain.
Here is the result:

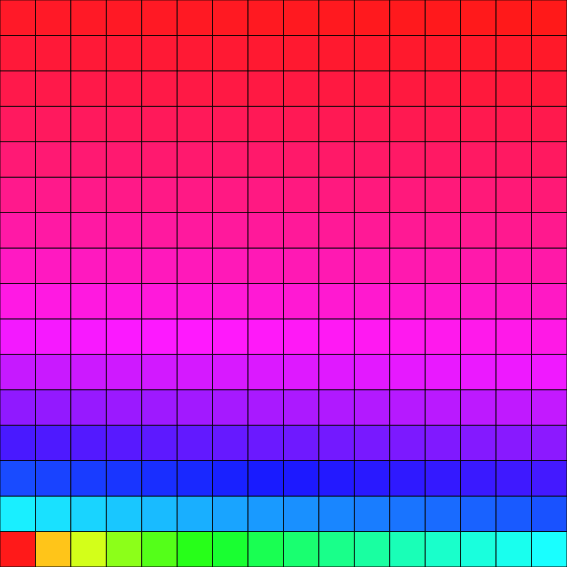
Here is now the construction of an image adapter that is a thresholded view of the initial scalar image:
and here is the result with a simple GrayscaleColorMap varying from 0 to 1:

Here is finally the construction of an image adapter that use a functor to change 'unsigned char' values to 'double' values using a log scale functor defined like that:
defined from the initial image:
and here is the result with a simple HueShadeColorMap varying from 0. to logScale(255):
ImageAdapter
ImageAdapter is a small class that adapts an image (like ConstImageAdapter) but provides a virtual access (reading and writing) of the true values contained in the adapted image. It uses a given Domain (i.e. a subdomain) but work directly (for reading and writing processes) thanks to an alias (i.e. a pointer) on the original Image given in argument.
This class requires an additional templare paremter: TFunctoVm1: functor to convert adapted image values to the original image values.
The values associated to accessing the point values are adapted
with a functor g and a functor f given at construction so that operator() calls f(img(g(aPoint))), instead of calling directly operator() of the underlying image img.
The values associated to writing the points are adapted
with a functor g and a functor \( f^{-1}\) given at construction so that setValue() is img.setValue(g(aPoint), f-1(aValue)).
The use is the same that for ConstImageAdapter.
ArrayImageAdapter
The ArrayImageAdapter class is less generic than ImageAdapter but is able to adapt any storage that have a random-access iterator to a concepts::CImage model. It is thus usable on C-style array but also on STL container like std::vector (and therefore on ImageContainerBySTLVector) and on another ArrayImageAdapter instances.
In addition, this class allows to restrict the visibility to a sub-domain of the definition domain and provides a read-write random-access iterator (depending on the mutability of the storage's iterator) with fast access to the underlying point (no need to iterate over the domain).
A common usage of this last feature is for padded raw data.
In order to illustrate the following ArrayImageAdapter usages, we need some common includes:
and the next definitions:
From a C-style array, we can create an image that spans the full definition domain:
and fill it using common iterator syntax:
that gives us the following result:

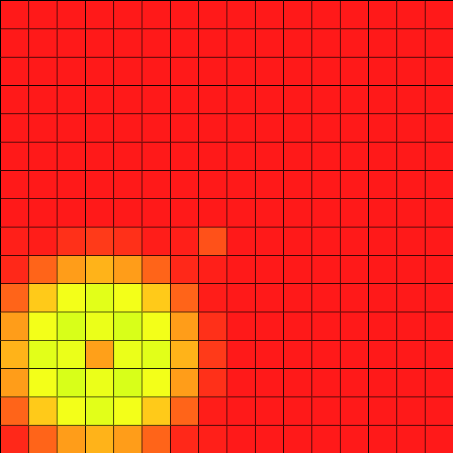
We can now create a read-only view of the same image on a sub-domain:
that gives us:
If we want to modify the image through this adapter, we must create a read-write instance using the following syntax:
or the alternate method using the helpers:
and we can then modify it using the common syntax with a domain iterator:

Alternatively, there is a computationally faster syntax (no need to linearize the point) using the method getPoint featured by the ArrayImageAdapter iterators (see ArrayImageIterator):

It is also possible to use ArrayImageAdater on any image model that provides a random-access iterator, like ImageContainerBySTLVector:
and adapt it using:
or, thanks to the helpers:
From there, we can use all the previous features or, for example, use available STL algorithms:
Useful classes and functions
In addition to the image containers and the image adapters described in the previous sections, there are also image proxys:
Image is a light proxy on image containers based on a COW pointer. It can be constructed, copied, assigned, deleted without any special care.
Moreover, in ImageHelper.h, many useful functions are provided.
- Conversely, others convert images into digital sets with value comparators: setFromPointsRangeAndPredicate, setFromPointsRangeAndFunctor, setFromImage.
- Some of them convert digital sets into images, imageFromRangeAndValue assigns a given value in an image to each point of a given range.
- Some functions are available to fastly fill images from point functors or other images: imageFromFunctor and imageFromImage.
- Lastly, some functor like the Projector from BasicPointFunctors can be useful to manipulate domain points and permits to extract N-1 images from ND images (see example extract2DImagesFrom3D.cpp).
Subsampling functor
In association with ConstImageAdapter or ImageAdapter you can apply image subsampling using a domain subsampler (BasicDomainSubSampler from the BasicPointFunctors class). The example imageBasicSubsampling.cpp illustrates such a simple image subsampling (in 2D and 3D).
To apply the subsampling, you first have to import the headers associated with the ConstImageAdapter and to the BasicDomainSubSampler:
Then you can define some image types including the ConstImageAdapter:
A subsampling functor can be constructed from a given grid size and a shift vector:
Afterwards the ConstImageAdapter can be defined as follows:
The resulting image can be exported with the GenericWriter class:
You will obtain such a result (with also the result on 3D images):

.
Constant image from a function, functor or lambda
If you need to define an image as the result of a callable object (function, functor or lambda) and you don't want to precalculate it or to store it, you should consider using the functors::ConstImageFunctorHolder class.
An instance of this class must be constructed through the associated helper functors::holdConstImageFunctor and you can use any callable object that accepts a point alone or a point and a domain (in order to have a domain dependent image definition).
A first usage example should be composed of the appropriate include:
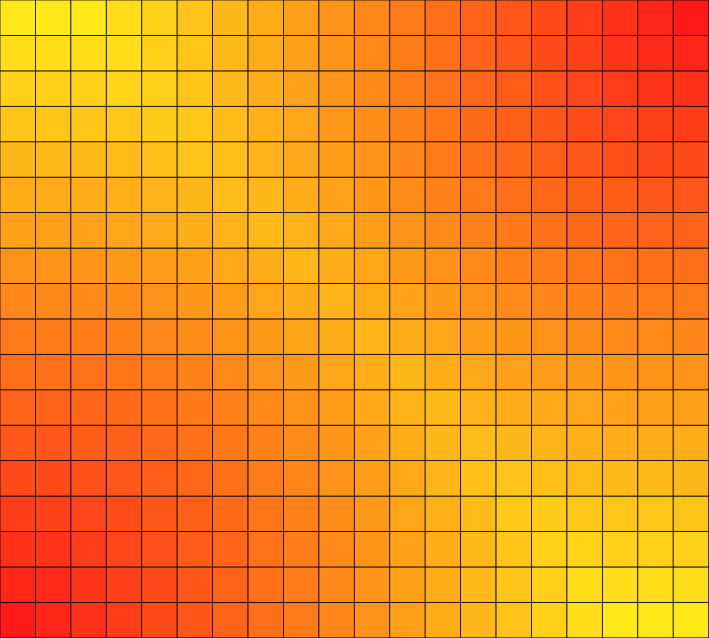
followed by the image definition:
that gives us the following result:
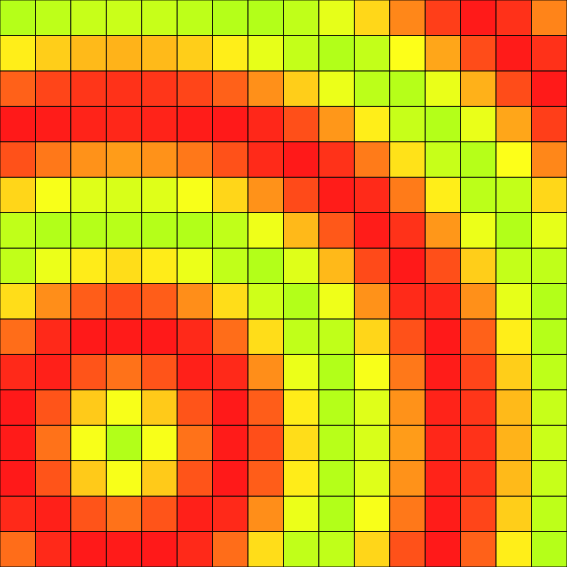
You can also use a functor that depends on the point and the image's domain:
resulting in:
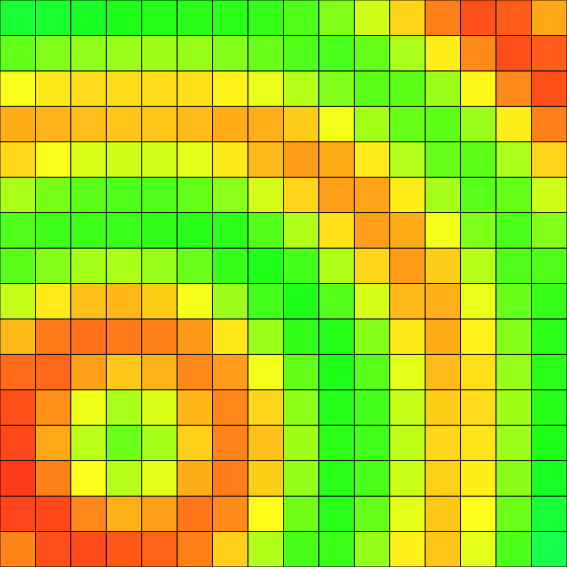
Going further, you can also capture other images in the lambda so that to define a mix:
resulting in:
- See also
- FunctorHolder, Using functions, functors and lambdas in DGtal